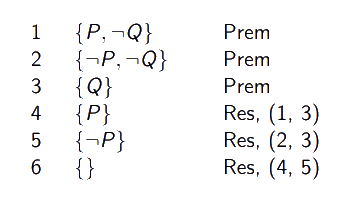Lógica Proposicional aplicada a sistemas computacionais

Voltamos a considerar a lógica proposicional, mas desta vez feita sob a perspetiva da sua utilização por sistemas computacionais, não por humanos. A geração automática de provas utilizando sistemas de dedução natural não é fácil, pelo que foram desenvolvidos métodos para a automatização da geração de provas. Um deles é a resolução, conceito que vai acompanhar-nos durante boa parte da cadeira.

Resolução

Abordagem ao sistema dedutivo baseada numa única regra de inferência (ao contrário das provas abordadas anteriormente) - o princípio da resolução. A utilização deste princípio obriga à transformação das fbfs numa forma especial, a forma clausal, que corresponde a uma conjunção de cláusulas.

Forma clausal

• Literal - uma fbf atómica ou (a sua negação) é chamada uma literal. Um literal positivo é uma fbf atómica não negada, sendo que um negativo é uma fbf negada. Importante relembrar que uma fbf atómica corresponde a uma fbf composta por um símbolo de proposição, não contendo quaisquer conectores lógicos.

• Cláusula - um literal/disjunção de literais. Caso consista em apenas um literal, podemos chamá-la cláusula unitária. Pode ainda ser representada como um conjunto (através do uso de chavetas) de literais.

Exemplo - Literais + cláusulas

Sendo $P$ e $Q$ símbolos de proposição, $P$ e $\neg Q$ são literais (positivo e negativo, respetivamente); $P$, $P\vee Q$, $\neg P\vee Q$ e $\neg Q$ são cláusulas, sendo que a primeira e a última são cláusulas unitárias.

A cláusula unitária $P$ pode ser representada como um conjunto tal que $\{P\}$. A cláusula $P\vee Q$ pode ser representada como um conjunto tal que $\{P, Q\}$.

Uma fbf diz-se na forma conjuntiva normal caso seja da forma $\alpha\wedge\beta\wedge\dots\wedge\gamma$, onde $\alpha, \beta,\dots,\gamma$ são obrigatoriamente cláusulas, unitárias ou não.

Exemplo - Forma conjuntiva normal

A fbf $(P\vee\neg Q\vee R)\wedge(\neg P\vee S)$ está na forma conjuntiva normal. A mesma fbf pode ser representada como um conjunto tal que $\{\{P, \neg Q, R\}, \{\neg P, S\}\}$.

Transformação de uma fbf em forma clausal

As fbfs podem, contudo, não nos ser apresentadas inicialmente nesta forma de disjunção de literais. É, portanto, importante ter e usar algoritmos e estratégias que nos permitam passar fbfs para o seu equivalente na forma clausal.

• Passos para a transformação de uma fbf em forma clausal

  Eliminar o símbolo $\to$

  Passo baseado na equivalência ($\alpha\to\beta$) $\leftrightarrow$ ($\neg\alpha\vee\beta$).

  Exemplo - Eliminar o símbolo $\to$

  Partindo de $P \to \neg(Q \vee ((R \wedge S) \to P))$:

  $\neg P \vee \neg(Q \vee ((R \wedge S) \to P))$;

  $\neg P \vee \neg(Q \vee (\neg(R \wedge S) \vee P))$.

  Reduzir o domínio do símbolo $\neg$

  Em forma clausal, nunca queremos que a forma final $\neg$ envolva a cláusula toda; por outro lado, não há qualquer problema em negar literais, pelo que aproveitamo-nos disso através de algumas regras úteis.

  • Lei da Dupla Negação

  $\neg\neg\alpha \leftrightarrow \alpha$

  • Primeiras Leis de De Morgan

  $\neg(\alpha\vee\beta) \leftrightarrow (\neg\alpha\wedge\neg\beta)$
  $\neg(\alpha\wedge\beta) \leftrightarrow (\neg\alpha\vee\neg\beta)$

  Exemplo - Reduzir o domínio de $\neg$

  Partindo de $\neg P \vee \neg(Q \wedge \neg(\neg(R \wedge S) \vee P))$:

  Aplicar as primeiras leis de De Morgan:

  $\neg P \vee \neg(Q \wedge (\neg\neg(R \wedge S) \wedge \neg P))$;

  Aplicar a Lei da dupla negação

  $\neg P \vee \neg(Q \wedge ((R \wedge S) \wedge \neg P))$;

  Obtenção da forma conjuntiva normal

  Baseia-se na equivalência $\alpha\vee(\beta\wedge\gamma)\leftrightarrow(\alpha\vee\beta)\wedge(\alpha\vee\gamma)$ para tornar disjunções em conjunções de disjunções, que estão na forma conjuntiva normal.

  Exemplo - Obter a forma conjuntiva normal

  Partindo de $(\neg P \vee \neg Q) \wedge (\neg P \vee ((R \wedge S) \wedge P))$:

  $(\neg P \vee \neg Q) \wedge (\neg P \vee (R \wedge S)) \wedge (\neg P \vee P)$;

  $(\neg P \vee \neg Q) \wedge (\neg P \vee R) \wedge (\neg P \vee S) \wedge (\neg P \vee P)$.

  Eliminar o símbolo $\wedge$

  Transformar a fbf já na forma conjuntiva normal num conjunto de cláusulas.

  Exemplo - Eliminar o símbolo $\wedge$

  Partindo de $(\neg P \vee \neg Q) \wedge (\neg P \vee R) \wedge (\neg P \vee S) \wedge (\neg P \vee \neg P)$:

  $\{\neg P \vee \neg Q, \neg P \vee R, \neg P \vee S, \neg P \vee \neg P\}$.

  Eliminar o símbolo $\vee$

  Transformar cada cláusula num conjunto de literais.

  Exemplo - Eliminar o símbolo $\vee$

  Partindo de $\{\neg P \vee \neg Q, \neg P \vee R, \neg P \vee S, \neg P \vee \neg P\}$:

  $\{\{\neg P, \neg Q\}, \{\neg P, R\}, \{\neg P, S\}, \{\neg P\}\}$

  O princípio da resolução é, portanto, uma regra de inferência derivada que é aplicável a cláusulas, gerando novas cláusulas.

  • Princípio da Resolução - sejam Ψ e Φ duas cláusulas e $\alpha$ uma fbf atómica, tal que $\alpha \in$ Ψ e $\neg\alpha \in$ Φ. Nesse caso, é possível inferir a cláusula (Ψ - {$\alpha$}) $\cup$ (Φ - {$\neg\alpha$}). A cláusula obtida é chamada o resolvente das cláusulas Ψ e Φ, representado por Res(Ψ, Φ), as quais são designadas cláusulas-mãe. Os literais $\alpha$ e $\neg\alpha$ designam-se literais em conflito.

  Na teoria pode parecer bastante confuso - o exemplo abaixo pretende desmistificar qualquer dificuldade que possa aparecer associada à resolução.

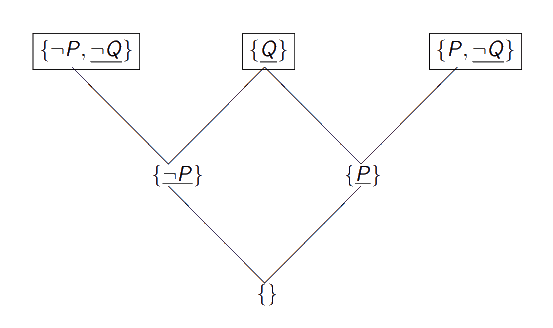
  Exemplos - Princípio da resolução

  Considerando as cláusulas $\{\neg P, Q, S\}$ e $\{P, \neg Q\}$:

  O seu resolvente-P é $\{Q, S, \neg Q\}$; (removemos os literais $P$ e $\neg P$ em conflito)
  O seu resolvente-Q é $\{\neg P, S, P\}$; (removemos os literais $Q$ e $\neg Q$ em conflito)

  Usando resolução, e procurando provar que $\{P, P \to Q\} \vdash Q$:

  • Passar à forma clausal: $\{P\}$, $\{\neg P, Q\}$ e $\{Q\}$;

  • Aplicar a resolução:

    $$\def\arraystretch{1.5} \begin{array}{lll} 1 & \{P\} && Prem\\ 2 & \{\neg P, Q\} && Prem\\ 3 & \{Q\} && Res(1, 2) \end{array}$$

  Podemos ainda realizar resoluções mais extensas:

  Mostrar que $\{\{\neg P, Q\}, \{\neg P, \neg Q\}, \{P\}\} \vdash \{\}$:

  $$\def\arraystretch{1.5} \begin{array}{lll} 1 & \{\neg P, Q\} && Prem\\ 2 & \{\neg P, \neg Q\} && Prem\\ 3 & \{P\} && Prem\\ 4 & \{Q\} && Res(1, 3)\\ 5 & \{\neg Q\} && Res(2, 3)\\ 6 & \{\} && Res(4, 5) \end{array}$$

  A cláusula vazia corresponde à existência de uma contradição.

  Normalmente a resolução aplica-se a provas por absurdo, as quais, utilizando a resolução, se chamam provas por refutação.

  • Provas por refutação - uma prova por refutação a partir de um conjunto de cláusulas $\Delta$ é uma prova por resolução de { } a partir de $\Delta$. O último exemplo do princípio da resolução corresponde a uma prova por refutação.

Estratégias em Resolução

Numa prova por resolução, a decisão sobre quais as cláusulas a utilizar em cada passo da prova deve ser tomada recorrendo a uma estratégia de resolução.

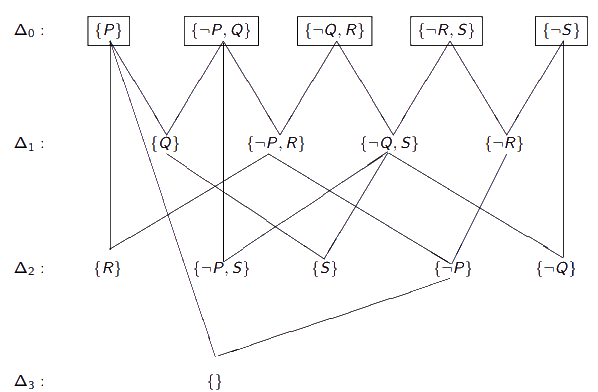
• Geração por saturação de níveis

  Consiste em separar as cláusulas geradas em vários níveis, cada um dos quais utiliza pelo menos uma das cláusulas existentes no nível anterior e gerar todas as cláusulas de um nível antes de começar a gerar as do próximo nível. Em suma, partindo de um conjunto de cláusulas inicial $\Delta$, criar um conjunto seguinte de todos os resolventes possíveis $\Delta_{1}$, repetindo até gerar ou o objetivo ou a cláusula vazia.

  VANTAGENS VS DESVANTAGENS

  Vantagem - fornece um algoritmo que garante encontrar uma solução, se esta existir, que corresponde ao menor número de aplicações do princípio da resolução.
  Desvantagem - gera muitas cláusulas que acabam por ser inúteis para a prova.

  Exemplo - Geração por saturação de níveis

  

Para aumentar a eficiência da geração de provas por resolução, foram desenvolvidas estratégias que se dividem em estratégias de eliminação/seleção de cláusulas.

• Estratégias de Eliminação de Cláusulas

  Passam por eliminar teoremas, cláusulas não mínimas (ou subordinadas) e literais puros.

  Eliminação de Teoremas

  Corresponde à eliminação das cláusulas que contenham tanto $\alpha$ como $\neg\alpha$, sendo $\alpha$ um símbolo de proposição. Porquê? Porque para quaisquer fbfs $\alpha$ e $\beta$, ($\alpha \vee \neg\alpha) \vee \beta$ é um teorema. Ora, um teorema não afetará o resultado final, visto que se $\Delta \cup {τ} \vdash \gamma$, então $\Delta \vdash \gamma$.

  Antes de abordar a eliminação de cláusulas não mínimas, interessa olhar para a definição de subordinação. Uma cláusula Ψ subordina Φ caso Ψ $\subseteq$ Φ.

  Eliminação de cláusulas não mínimas

  Dado um conjunto de cláusulas, podemos eliminar todas as cláusulas subordinadas/não mínimas por uma outra cláusula existente no conjunto.

  Exemplo - Eliminar teoremas/cláusulas não mínimas

  Considerando as cláusulas $\{\{\neg P, \neg Q, R\}, \{\neg P, \neg Q, Q\}, \{\neg P, \neg Q\}\}$, podemos aplicar a eliminação de teoremas e ficar com $\{\{\neg P, \neg Q, R\}, \{\neg P, \neg Q\}\}$: ter $Q$ e $\neg Q$ na mesma cláusula é inconclusivo, não ficamos a saber nada sobre a mesma porque esta será sempre verdadeira.

  Posteriormente, podíamos ainda eliminar cláusulas não mínimas, ficando apenas com $\{\{\neg P, \neg Q\}\}$. Esta eliminação segue a lógica de: se temos $\neg P \vee \neg Q$, será irrelevante ter $\neg P \vee \neg Q \vee R$, porque temos "mais informação" sobre os valores lógicos associados a literais concretos em cláusulas mais pequenas.

  Dizemos que é mais simples tentar descobrir qual dos literais em $A \vee B$ tem valor lógico verdadeiro do que tentar descobrir o mesmo numa cláusula com 20 literais.

  Para olhar para a eliminação de literais puros, temos primeiro de definir literal puro - um literal diz-se puro quando apenas o próprio literal (ou apenas a sua negação) aparece num dado conjunto de cláusulas.

  Exemplo - Literais puros

  Dado o conjunto de cláusulas $\{\{P, Q, \neg R\}, \{P, \neg Q, \neg R\}\}$, $P$ e $R$ são literais puros.

  Ora, se um literal é puro, não nos será útil durante provas por refutação, visto que não o poderemos eliminar por resolução. Assim sendo, podemos remover as cláusulas que o contêm.

  Eliminação de Literais Puros

  Podemos remover todas as cláusulas que contenham literais puros. Esta estratégia é, ao contrário das últimas duas, realizada apenas uma vez, no início da prova por refutação.

• Estratégias de Seleção de cláusulas

  Corresponde a um processo de controlar as cláusulas geradas numa prova por resolução, impondo restrições às cláusulas que podem ser candidatas à aplicação do princípio da resolução. Aqui, consideramos as resoluções unitária e linear.

  Resolução unitária

  Baseia-se no facto de ao utilizarmos a resolução tentarmos por norma diminuir o número de literais existentes nas cláusulas produzidas (mais evidente em provas por refutação, onde tentamos chegar à cláusula vazia). Se uma das cláusulas envolvidas numa aplicação do princípio da resolução apenas contiver um literal, uma cláusula unitária, é então garantido que o resolvente tem menos literais do que a cláusula mãe com maior número de literais. Esta estratégia consiste, portanto, em aplicar o princípio da resolução utilizando sempre pelo menos uma cláusula unitária. Nem todas as proposições válidas podem ser provadas desta maneira, visto que nem sempre estamos na presença de cláusulas unitárias. Não é, portanto, um processo de inferência completo.

  Exemplo - Resolução unitária

  

  

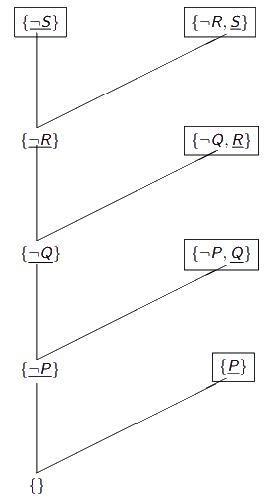
  Resolução Linear

  Começamos por selecionar uma cláusula entre as premissas, a cláusula inicial, obtendo um resolvente entre a cláusula inicial e outra qualquer pertencente às premissas. A partir daí, sempre que se aplica o princípio da resolução utiliza-se o último sucessor da cláusula inicial. Qualquer sucessor da cláusula inicial chama-se cláusula central. Geralmente como cláusula inicial escolhemos a que corresponde à negação da cláusula que pretendemos provar, usando portanto a prova por refutação. Nesta prova por refutação, adicionaríamos a negação da conclusão ao conjunto de premissas, e tentaríamos derivar { }.

  Exemplo - Resolução Linear

  Para provar que $\{\{\neg P, Q\}, \{\neg Q, R\}, \{\neg R, S\}, \{P\}\} \vdash \{S\}$, começamos por transformar a prova em $\{\{\neg P, Q\}, \{ \neg Q, R\}, \{\neg R, S\}, \{P\}, \{\neg S\}\} \vdash \{ \}$.
  Uma vez que estamos a tentar provar $S$, utilizamos $\{\neg S\}$ como cláusula inicial.

  

• Correção e completude da resolução

  A resolução é correta mas não completa. Não é possível demonstrar todos os argumentos válidos. Contudo, a resolução é completa no que à refutação diz respeito, visto que podemos sempre derivar a cláusula vazia caso o conjunto inicial de cláusulas seja insatisfazível.